基本関数に戻る    印刷する

算術計算

図形を円の軌跡の上で動かしたり、振動させたりするときに、三角関数が役立ちます。また偶然の要素を入れた動きをさせたいとき、乱数が必要になります。さまざまな算術計算のための関数が提供されています。

乱数

サイコロの目が同じ確率で出るように、同じ確率で、指定した範囲の数をひとつ返します。引数は整数(int型)あるいは実数(float型)で指定します。
■ random(high)　　0とhighの間の乱数が実数(float型)で得られます。
■ random(low, high)　　low とhighの間の乱数が実数(float型)で得られます。

【例】random(1.2, 10)　　1.2と10の間のいずれかの数を返す。

整数の乱数がほしい場合は、整数を作り出す関数int( )の引数に、乱数random()を指定します。すると作り出された乱数の整数部分だけがとり出されます。

【例】int a;
      a = int(random(6)); 　0,1,2,3,4,5のいずれかの値がaに入る。

三角関数

三角関数の計算をします。引数のangleにはラジアン単位の角度を実数(float型)で指定します。radians(角度)を使って、度単位の角度をラジアン単位に変換できます。

■ sin(angle)　　angleのsinの値を計算する。結果はfloat型で-1から1の間の値。
■ cos(angle)　　angleのcosの値を計算する。結果はfloat型で-1から1の間の値。

次のリストは、直径100の円周上で、小さい円を動かす例です。
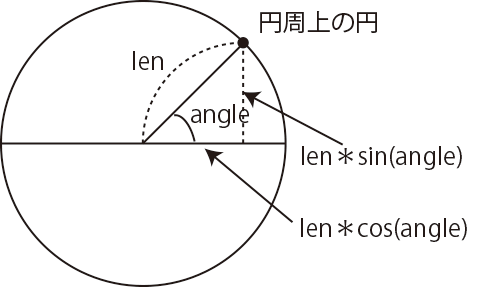
円周上の座標は右の図のように、sin()関数と、cos()関数を使って計算できます。これら関数の引数は円周上の点の、円の中心からみた角度です。円周上時計の3時の位置が角度0度で、時計回りに角度が大きくなります。

【リスト　三角関数：円周上を移動】
float r = 50;
float a = 0; //角度(度単位)
float x, y;
void setup() {
  size(150,150);
  fill(200,0,0);
  noStroke();
  background(255);
}
void draw() {
  translate(width/2, height/2);  //座標原点を画面の中央へ移動
  x = r * cos(radians(a)); //円周上a度の位置のx座標を計算
  y = r * sin(radians(a)); //円周上a度の位置のy座標を計算
  ellipse(x, y, 10, 10);  //画面中央に円
  a = a + 1; //1度ずつ右へ回る
}

上のプログラムでは、a = a + 1;と、angleはプログラムが動き続けている間、増加し続けます。angleはfloat型の変数で、そこに入る値の最大値は、3.40282347E+38(E+38は10の38乗の意味)です。aの中の値が増加し続けて、この最大値を超えると、最小値(-3.40282347E+38)に戻ります。そのため動作には支障はありません。

■ tan(angle)　　angleのtanの値(sinとcosの比率)を計算します。結果はfloat型で-無限大から無限大の間の値。
■ atan2(y, x)　　指定された点の中心から見た角度を計算します(x軸の正方向が0度)。結果はラジアン単位の角度で、-π(PI)からπの間の値(float型)。

次のリストは、マウスで長方形を回転させる例ですが、画面中央からみたマウスの角度の計算にatan2()関数を使っています。 atan2()関数の引数にはマウス位置を指定しますが、mouseX, mouseYの値は、左上角を原点とした時の座標であるため、中央を原点とした座標に換算しています。

【リスト　三角関数：マウスについて回転】
int w = 80; //四角形の幅
int h = 10; //四角形の高さ
void setup() {
  size(125,125);
}
void draw() {
  background(255);
  translate(width/2, height/2);  //座標原点を画面の中央へ移動
  float a = atan2(mouseY-height/2, mouseX-width/2); //画面中央からみた角度を計算。
  //引数は、画面中央を原点としたマウスの位置。
  rotate(a);  //マウスの位置に応じて回転
  rect(-w/2, -h/2, w, h);  //長方形を描く。長方形がマウスで回転する。
  ellipse(0, 0, 10, 10);  //画面中央に円
}

対数・指数

引数には実数(float型)の値を指定します。
■ exp(n)　　自然対数、e(2.71828...)を底とする対数の値(float型)を返します。
■ log(n)　　自然指数、e(2.71828...)を底とする指数の値(float型)を返します。

四捨五入・切り捨て・切り上げ

引数には実数(float型)の値を指定します。
■ round(n)　　nに一番近い整数を返します(四捨五入する)。
■ floor(n)　　nより小さいか等しい整数を返します(小数点以下を切り捨てる)。
■ ceil(n)　　nより大きいか等しい整数を返します(小数点以下を切り上げる)。

最大値・最小値・値の制限

引数には、整数(int型)あるいは実数(float型)の値を指定します。listはデータの列(配列、float[]またはint[])。
■ max(a, b)　　aとｂで大きい値を返します。
■ max(a, b, c)　　a,b,cで一番大きい値を返します。
■ max(list)　　データのリスト(配列)の中で一番大きい値を返します。
■ min(a, b)　　aとｂで小さい値を返します。
■ min(a, b, c)　　a,b,cで一番小さい値を返します。
■ min(list)　　データのリスト(配列)の中で一番小さい値を返します。
■ constrain(a, low, high)　　値aが最小値lowと最大値highの間を越えないように制限します。
■ abs(a)　　値aの絶対値を返します。

距離の計算

2つの点の間の距離を計算します。引数には実数(float型)の値を指定します。計算結果も実数(float型)です。
■ mag(a, b)　　座標原点から点(a,b)までの距離を計算。
■ dist(x1, y1, x2, y2)　　点(x1,y1)と点(x2,y2)の間の距離を計算。

値の換算

比例換算をする関数です。引数には実数(float型)の値を指定します。計算結果も実数(float型)です。
■ lerp(v1, v2, a)　　v1とv2の間の比率aの位置の値を計算。aの値は0-1.0。aが0なら、計算結果はv1と同じ。
■ norm(v, start, stop)　　startとstopの間の値vを0－1.0の値に変換します。map(value, start, stop, 0, 1)と同じ計算になります。
■ map(v, start1, stop1, start2, stop2) 　　start1とstop1の間の値vを、別の範囲start2とstop2の間の値に変換します。